Hi-kvadrat test u Excel-u

χ2-test (hi-kvadrat) je vrlo praktičan test kojeg generalno koristimo kada želimo utvrditi odstupaju li neke dobivene (opažene) frekvencije od frekvencija koje bismo očekivali pod određenom hipotezom. Primjena u poslovnoj statistici uglavnom se svodi na rješavanje dviju skupina problema, koje navodimo s primjerima.

Test nezavisnosti dviju varijabli. Ponekad, na temelju podataka iz uzorka, želimo znati s kojom sigurnošću možemo tvrditi da su neke dvije varijable povezane. Pritom se uglavnom radi o kvalitativnim, odnosno kategorijalnim varijablama. Može nas, na primjer, zanimati ovisi li sklonost kupnji određenog proizvoda o spolu, primanjima ili nekoj drugoj karakteristici kupca. Ili, primjerice, pokazuje li drugačiji pristup nekom poslu statistički značajne drugačije rezultate. 

Test pripadnosti distribuciji. Pomoću hi-kvadrat testa možemo provjeriti u kojoj mjeri podaci iz uzorka podupiru pretpostavku da promatrana slučajna varijabla ima neku pretpostavljenu distribuciju (razdiobu). Na primjer, autobusni prijevoznik želi na uzorku od nekoliko desetaka vožnji na linijama koje održava provjeriti uvriježeno mišljenje da postotak popunjenosti autobusa ima normalnu distribuciju s prosjekom 85% i standardnom devijacijom 6%. Naime, to saznanje želi primjeniti u poslovnom planiranju pa želi biti u dovoljnoj mjeri siguran da je to stvarno tako.

Kako su u MS Excel ugrađene sve potrebne statističke funkcije, Hi-kvadrat test se u Excelu provodi relativno jednostavno. Posebno brzo i jednostavno se može, na pripremljenim tablicama opaženih i očekivanih distribucija, napraviti test nezavisnosti pomoću funkcije CHISQ.TEST.

U nastavku ćemo po koracima prikazati provedbu jednog takvog testa na primjeru.

Primjer: Utječe li boja promotivnog letka na to hoće li ga prolaznici uzeti?

Distribuirani su promotivni letci koji su tiskani u tri različite boje: bijeloj, svijetloplavoj i ružičastoj. Želimo provjeriti postoji li učinak boje letka na odluku prolaznika hoće li letak uzeti, ili će ga ignorirati.

Podaci iz uzorka, kojeg je činilo 150 prolaznika, grupirani su po dvije promatrane varijable u tablicu kontingencije:

Iz zbrojeva u zadnjem stupcu vidimo da je od 150 prolaznika letak uzelo njih 90. U zadnjem retku tablice vidljivo je koliko je prolaznika bilo izloženo kojoj boji letka. Vidljivo je i da omjer broja prolaznika koji su letak uzeli i onih koji nisu, varira od boje do boje. Iz toga izvodimo slutnju da boja letka ima utjecaja na odluku prolaznika o tome hoće li ga uzeti. Međutim, oprezni smo u donošenju zaključka jer se ipak radi o uzorku. Postoji mogućnost da je ta razlika u omjerima nastala slučajno, zbog odabira upravo ovog uzorka od 150 prolaznika, a ne nekog drugog (od vrlo velikog broja mogućih uzoraka veličine 150).

Stoga će naša početna pretpostavka (hipoteza) biti da, u populaciji kojoj se obraćamo u promotivnoj kampanji, boja letka nema utjecaja na odluku prolaznika o uzimanju. To bi podrazumijevalo da su gore opažene frekvencije koje sugeriraju da boja ima utjecaja, posljedica uzorkovanja. Naime, u jako velikom broju uzoraka veličine 150 koje je moguće na slučajan način dobiti iz populacije, neki od njih će pokazivati znatne razlike u spomenutim omjerima 'uzeo/nije uzeo' po bojama, čak i ako u populaciji boja generalno ne utječe na odluku. Uloga Hi-kvadrat testa je da nam kaže koja je vjerojatnost da se u takvoj populaciji pojavi takav uzorak. Ako je ta vjerojatnost jako mala, onda ćemo s velikim stupnjem sigurnosti zaključiti da naš uzorak ipak nije došao iz populacije u kojoj boja nema utjecaja na odluku. U tom slučaju ćemo odbaciti početnu hipotezu o populaciji i prihvatiti alternativnu, odnosno zaključit ćemo da boja letka ima utjecaja na odluku prolaznika o uzimanju.

Slijedeći našu pretpostavku o populaciji u kojoj boja letka ne utječe na odluku o uzimanju, formiramo tablicu očekivanih (teoretskih) frekvencija:

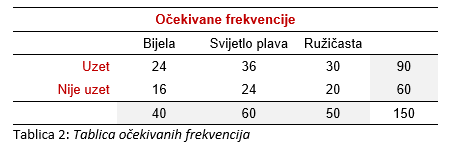
Objasnit ćemo na primjeru frekvencije 24 kako se računaju očekivane frekvencije. Kako je od 150 prolaznika (kada se gledaju letci svih boja) letak uzelo njih ukupno 90, postotak uzimanja je 90/150, tj. 60%. Bijelih letaka u uzorku je bilo 40, pa bi njih trebalo biti uzeto 60% od 40, što iznosi 24. Na isti način su izračunate sve očekivane frekvencije. Zbroj po bojama i po odlukama odgovara zbrojevima iz tablice opaženih frekvencija.

Što je razlika između opaženih i očekivanih frekvencija veća, manja je vjerojatnost da naš uzorak (opažene frekvencije) dolazi iz pretpostavljene populacije, dakle one u kojoj boja letka nema utjecaja na odluku o uzimanju.

Tu vjerojatnost, tzv. p-value, dobit ćemo korištenjem funkcije CHISQ.TEST. Pritom kao prvi argument funkcije unosimo raspon u kojemu se nalaze opažen frekvencije, a kao drugi raspon u kojemu se nalaze očekivane frekvencije.

=CHISQ.TEST(C4:E5;C11:E12).

Rezultat za naš primjer je 0,00048. To znači da bi se, uz pretpostavku da u populaciji boja letka nema utjecaja na odluku o uzimanju, uzorak sa takvim razlikama u frekvencijama u odnosu na očekivane poput našeg, pojavio u 0,048% slučajeva. Kako se radi o jako maloj vjerojatnosti, zaključujemo da polaznu pretpostavku o populaciji treba odbaciti i prihvatiti suprotnu, tj. da u ciljanoj populaciji boja letka ima utjecaj na odluku.

Drugi pristup hi-kvadrat testu, je da se na temelju razlika između opaženih i očekivanih frekvencija izračuna vrijednost Hi-kvadrat statistike, te usporedi s kritičnom vrijednošću. Kritična vrijednost očitava se iz tablica ili računa pomoću Excel funkcije CHISQ.INV.RT. Ovaj pristup se obično primjenjuje ako je unaprijed zadana neka razina značajnosti npr. 0,05 ili 0,01. Razinu značajnosti možemo shvatiti kao prihvatljivu vjerojatnost pogreške (u smislu da vidimo utjecaj kojeg u stvari nema).

Vrijednost hi-kvadrat statistike računa se tako da se zbroje omjeri kvadrata razlike opaženih i očkivanih frekvencija i očekivanih frekvencija. To se može napraviti kreiranjem pomoćnih izračunskih tablica, a u našem primjeru dobiva se:

Kritična vrijednost određuje se na temelju zadane razine značajnosti i broja stupnjeva slobode. Broj stupnjeva slobode u ovakovom problemu računa se po formuli df=(m-1)(n-1), gdje je m broj redaka, a n broj stupaca tablice frekvencija.

Ako je zadana razina značajnosti 0,05 (5%), uz broj stupnjeva slobode 2, funkcija CHISQ.INV.RT kao kritičnu vrijednost za odbacivanje hipoteze daje broj 5,99. Kako je vrijednost hi-kvadrat statistike veća od kritične, odbacujemo hipotezu da u ciljanoj populaciji boja letka nema utjecaja na odluku o uzimanju letka.

Joško Meter, dipl. ing.